Commutative and Associative Properties of Addition

"Hi! I'm here with Amanda Bear today to talk about the Commutative Property of Addition. We're going to use this gum ball machine to demonstrate that buying a gum ball from a machine is not commutative."

ordofops

"Amanda wants some gum from this machine. Before she can get it; she must first put money into the machine. This is not a commutative operation. If it were, Amanda could get the gum ball and then put the money in the machine."

bad bear

"But if I use a hammer, the operation is commutative. I can get as many gumballs as I want and I don't have to pay for them if I don't want to."

oh no

"No! No! Amanda Your wrecking the demonstration. Oh well, read below for more on the Commutative Property."

*****

duane hyde

Victor de Velo was the lead rider for team La Française des Jeux in the 85th Tour de France, a bicycle race which takes place over three weeks and winds through the French countryside, past the coast, and over towering Alpine mountains.

To keep track of how far he has gone on two consecutive days, Victor can add the two distances in any order and the total remains the same.

This is called the Commutative Property of Addition.

For example, if the Prologue of the Tour is 5.6 km and Stage 1 is 180.5 km, Victor can add the distances in either order to get the total for the two days.

5.6 + 180.5 = 180.5 + 5.6 =186.1

To find the total for the first three days of the Tour, Victor would add 5.6 km + 180.5 km + 205.5 km. Following the rules for Order of Operations, we would do these additions from left to right. However, since they are all additions, we can do them in any order and still get the same answer.

This is called the
Associative Property of Addition.

duane hyde

5.6 + 180.5 + 205.5
(5.6 + 180.5) +205.5 = 5.6 + (180.5 + 205.5)
186.1 + 205.5 = 5.6 + 386
391.6 = 391.6

The Commutative Property (changing the order of the numbers)
and the Associative Property (changing the order of the additions) are important because they allow us to easily simplify expressions which contain only addition.

In the example above, the right side of the equation is easier because you can combine the second two decimal numbers into a whole number.

Because addition is commutative and associative, for any expression involving only addition, you can change the order of addends and add parentheses whenever you desire.

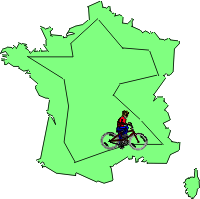Here is a page from Victor's racing journal. Tell which property he used to calculate the distance he rode:

Stage 3 = 169 km
Stage 4 = 252 km
Stage 5 = 228.5 km
Stage 6 = 204.5 km

A: Total for stages 3 & 4:
169 + 252 = 252 + 169 = 421

B: Total for stages 3, 4, & 5:
169 + 252 + 228.5 =
169 + (252 + 228.5) = 649.5

C: Total for stages 4, 5, & 6:
252 + (228.5 + 204.5) =
252 + (204.5 + 228.5) = 685

Number Theory Main | Commutative and Associative Properties of Multiplication

Written by: Nikki Siegel

Art by: Duane Hyde and Travis Spaid